Unser Volumenrechner ermöglicht die präzise Berechnung des Volumens verschiedener geometrischer Körper. Wählen Sie einfach die gewünschte Form aus und geben Sie die erforderlichen Maße ein. Ideal für Architekten, Ingenieure, Schüler und alle, die mit räumlichen Berechnungen arbeiten.
Volumenrechner
Wählen Sie eine geometrische Form und füllen Sie die Felder aus, um das Volumen zu berechnen:
Übersicht der Volumenformeln
| Geometrischer Körper | Formel | Benötigte Maße |
|---|---|---|
| Quader | \(V = l \times b \times h\) | Länge, Breite, Höhe |
| Würfel | \(V = a^3\) | Kantenlänge |
| Kugel | \(V = \frac{4}{3} \pi r^3\) | Radius |
| Zylinder | \(V = \pi r^2 h\) | Radius, Höhe |
| Kegel | \(V = \frac{1}{3} \pi r^2 h\) | Radius, Höhe |
| Pyramide | \(V = \frac{1}{3} G h\) | Grundfläche, Höhe |
Quader Volumen berechnen
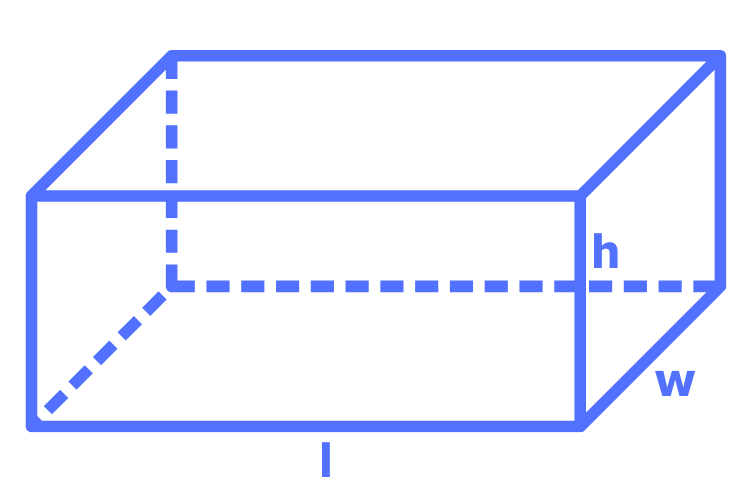
Ein Quader ist ein dreidimensionaler Körper mit sechs rechteckigen Flächen. Alle gegenüberliegenden Flächen sind dabei parallel und kongruent.

\(V = l \times b \times h\)
Infos zu den Variablen:
- l = Länge
- b = Breite
- h = Höhe
Würfel Volumen berechnen
Ein Würfel ist ein Spezialfall des Quaders, bei dem alle Kanten gleich lang sind. Er besitzt sechs quadratische Flächen gleicher Größe.

\(V = a^3\)
Infos zu den Variablen:
a = Kantenlänge
Kugel Volumen berechnen
Eine Kugel ist ein vollkommen symmetrischer Körper, bei dem alle Punkte der Oberfläche den gleichen Abstand zum Mittelpunkt haben.

\(V = \frac{4}{3} \pi r^3\)
Infos zu den Variablen:
- r = Radius
- π ≈ 3,14159
Zylinder Volumen berechnen
Ein Zylinder entsteht, wenn ein Kreis entlang einer geraden Linie durch den Raum bewegt wird. Er besitzt zwei parallele, kreisförmige Grundflächen.

\(V = \pi r^2 h\)
Infos zu den Variablen:
- r = Radius der Grundfläche
- h = Höhe
Kegel Volumen berechnen
Ein Kegel entsteht, wenn ein Dreieck um eine seiner Katheten rotiert. Er hat eine kreisförmige Grundfläche und verjüngt sich zu einer Spitze.

\(V = \frac{1}{3} \pi r^2 h\)
Infos zu den Variablen:
- r = Radius der Grundfläche
- h = Höhe
Praktische Anwendungsbeispiele
| Körper | Anwendungsbeispiel | Beispielrechnung |
|---|---|---|
| Würfel | Verpackungsvolumen | Kantenlänge 10 cm: \(V = 10^3 = 1000\text{ cm}^3\) |
| Zylinder | Wasserturm | r = 5 m, h = 10 m: \(V = \pi \cdot 5^2 \cdot 10 = 785,4\text{ m}^3\) |
| Kugel | Wassertank | r = 3 m: \(V = \frac{4}{3}\pi \cdot 3^3 = 113,1\text{ m}^3\) |
Tipps zur genauen Volumenberechnung
- Einheitenkonsistenz: Verwenden Sie stets die gleichen Maßeinheiten für alle Messungen
- Messgenauigkeit: Messen Sie alle erforderlichen Längen möglichst präzise
- Rundung: Runden Sie erst am Ende der Berechnung, nicht zwischendurch
- Kontrolle: Prüfen Sie, ob das Ergebnis plausibel erscheint
Mehr Tools für die Geometrie:
